به نقل از ساینس الرت، راه حل یکی از مسائل مهم حل نشده در حوزه ریاضیات، توسط سِر مایکل عطیه ریاضیدان مشهور جهان پیدا شد.
تدبیر24»عطیه که یکی از برجسته‌ترین ریاضیدانان بریتانیا است، راه حلی را برای
قضیه مشهور "ریمان" در انجمن برجسته هایدلبرگ در آلمان ارائه داد.
مایکل عطیه (Michael Atiyah) زاده ۲۲ آوریل ۱۹۲۹، توپولوژی و هندسه‌دان
اهل بریتانیا است. وی پس از به پایان بردن تحصیلات مقدماتی خود در سودان و
مصر برای تحصیلات دانشگاهی به انگلستان رفت و نهایتا تحت هدایت ویلیام هاج
از دوره دکتری فارغ‌التحصیل شد. پدر وی ادوارد سلیم عطیه نویسنده و فعال
سیاسی لبنانی-بریتانیایی بود.
عطیه همچنین برنده جوایزی همچون مدال فیلدز شده است که مانند جایزه نوبل در ریاضیات است.
عطیه در طول سخنرانی خود در انجمن هایدلبرگ گفت: "حدس ریمان" (Riemann
hypothesis) را حل کنید و معروف شوید. اگر هم از قبل معروف هستید، رسوا
خواهید شد!
وی افزود: هیچ کس باور نمی‌کند که هیچ مدرکی مبنی بر حل حدس ریمان وجود
داشته باشد، زیرا خیلی دشوار است. هیچ کس آن را ثابت نکرده است، پس چرا
باید کسی حالا آن را اثبات کند؟ البته مگر اینکه شما یک ایده کاملا جدید
داشته باشید.
این اظهارات، بحث‌های زیادی را در اینترنت و میان کارشناسان ریاضی ایجاد کرده است.
حدس ریمان چیست؟
حدس ریمان با اعداد اول یعنی آن اعدادی که تنها بر خودشان و ۱ قابل
تقسیم هستند، کار دارد. از زمان آغاز ریاضیات، همیشه حدس و پیش‌بینی اعداد
اولی که به صورت پیوسته در مجموعه اعداد اول می‌آیند، جذاب بوده است.
تا اینکه "برنهارد ریمان" با انتشار یک مقاله ۸ صفحه‌ای در سال ۱۸۵۹ یک پیشرفت عظیم در نظریه اعداد اول حاصل کرد.
وی به جای تلاش برای تعیین اعداد اول، به نمود اعداد اول نگاه کرد.
حدس ریمان توسط برنهارد ریمان ساخته شد که یک حدس در مورد ریشه‌های تابع
زتای ریمان است که می‌گوید ریشه‌های غیرساده این تابع بخش حقیقی آن‌ها
برابر ۰٫۵ (۱/۲) است. حدس ریمان یکی از مسائل هزاره است که برای حل آن
جایزه یک میلیون دلاری تعیین شده بود.
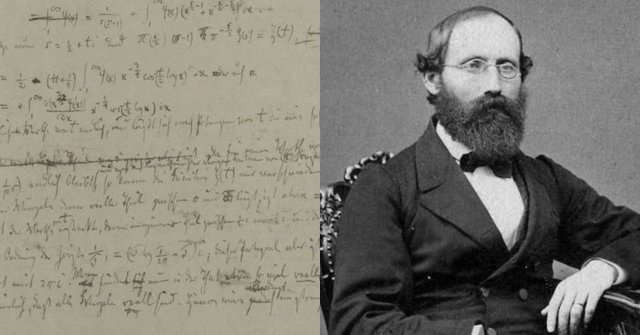
حدس ریمان نتایجی درباره توزیع اعداد اول دارد. این مسئله در میان بعضی
از ریاضیدان‌ها به عنوان یکی از مهمترین مسائل حل نشده در ریاضیات محض
شناخته می‌شد.
حدس ریمان بخشی از مسئله هشتم هیلبرت است که خود بخشی از ۲۳ مسئله حل
نشده است. با اینکه این مسئله، حل نشده بود، اما محاسبات رایانه‌ها نشان
داده بود که ۱۰ تریلیون ریشه ابتدایی این مسئله دارای مؤلفه بخش حقیقی
Re=۰.۵ هستند.
تابع ریمان زتا ζ. (s) برای تمامی اعداد مختلط s. s. ≠ ۱ تعریف می‌شود.
این تابع ریشه‌های در اعداد منفی زوج (یعنی -۲، ۴، ۶، ...) دارد که به آن
ریشه‌های ساده گفته می‌شود، اما تابع زتا ریشه‌های غیر ساده نیز دارد که
حدس ریمان می‌گوید تمامی این ریشه‌ها بر روی خطی قرار می‌گیرند که میزان
مقدار حقیقی آن برابر ۰٫۵ است که به آن خط بحرانی گفته می‌شود.
تاکنون نه تنها اثباتی برای این مسئله که تمام ریشه‌های غیر ساده تابع
زتا دارای بخش حقیقی ۰٫۵ است ارائه نشده بود، بلکه مثال نقضی نیز پیدا نشده
بود که تابع زتا در نقطه‌ای صفر باشد که بخش حقیقی آن نقطه ۰٫۵ نباشد.
اما سرانجام امروز دوشنبه دوم مهر ۱۳۹۷، حدس ریمان توسط مایکل عطیه اثبات شد
وی برای اثبات این حدس، از کار‌ها و راه‌حل‌های ریاضیدانانی به نام "جان
فون نیومان" و "فریدریش هایزربرو" که برای حل حدس ریمان انجام داده بودند،
استفاده کرده است و نشان داد که راه حل آن‌ها درست و قابل اثبات است.
عطیه توضیح داد: به نظر می‌رسد معجزه‌ای رخ داده است، اما ادعا می‌کنم که تمام کار‌های سخت ۷۰ سال پیش انجام شده بوده است.
"نیکلاس جکسون" از دانشگاه وارویک انگلستان می‌گوید: حدس ریمان یک مسئله
واقعا دشوار است. بسیاری از ریاضیدانان سطح بالا تقریبا در تمام طول این
سال‌ها به اثبات آن نزدیک شده‌اند، اما موفق نشدند و حتی نتوانستند یک مثال
نقض برای آن بیاورند.
اگر نظریه عطیه پابرجا بماند، او می‌تواند به یکی از مسن‌ترین ریاضیدانانی تبدیل شود که یک مسئله پیچیده ریاضی را اثبات کرده است.
ارسال به دوستان 
نسخه چاپی 
